Нейронные сети. Начало

2019-01-12 12:17

основы нейронных сетей

     Всем доброго времени суток. Нейросети в последнее время становятся все более и более популярными, потому не разобрать основы их работы я не могу.

Немного истории

     Как вы уже поняли из названия, нейронные сети появились в момент изучения работы биологических нейросетей - нервные системы живых организмов.

    Вся история началась с искусственного нейрона Маккалона-Пирса, который по математически является нелинейной функцией(функция активации) от суммы входных сигналов. По факту это упрощенный вариант биологического нейрона, из которых составляют отдельные сети.

Принцип работы

     Вспомним формулу линейной функции:

y = w[0] * x[0] + w[1] * x[1] + .... w[p] * x[p] + b

 Графически мы изобразим это так:

w[0..p] - веса узлов, x[0..p] - входные признаки. На рисунке изображена сеть без скрытого узла, который представляет собой ряд нейронов. Посмотрим, как это будет выглядеть с одним скрытым слоем.

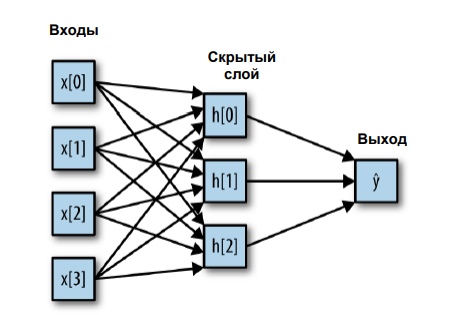
     Здесь намного больше весов - на каждый синапс(стрелочку, если смотреть на рисунок) приходится один вес. В скрытом слое у нас три нейрона, каждый из которых принимает взвешенную сумму всех признаков, обрабатывает результат с помощью функции активации и подает полученный результат на выход.

Если говорить языком математики, то(функция активации - f):

h[o] = f(x[0] * w[0] + x[1] * w[1] + x[2] * w[2] + x[3] * w[4])

h[1] = f(x[0] * w[5] + x[1] * w[6] + x[2] * w[7] + x[3] * w[8])

h[2] = f(x[0] * w[9] + x[1] * w[10] + x[2] * w[11] + x[3] * w[12])

А y вычисляется по формуле:

y = h[0] * v[1] + h[1] * v[1] + h[2] * v[2]

w - веса между входом и скрытым слоем, v - веса между скрытым слоем и выходом.

     Кол-во узлов в скрытом слое - очень важный параметр, который настраивает пользователь. Его значение может быть абсолютно разным и зависит от размера входных данных.

Обычно используют две нелинейные функции активации:

• выпрямленный линейный элемент (rectified linear unit)
• гиперболический тангенс(tanh)

     В NumPy эти функции имеют названия np.tanh(arg) и np.maximum(arg, 0).

      Построим графики этих функций на диапазоне (-3, 3), используя Jupyter Notebook:

Результат таков:

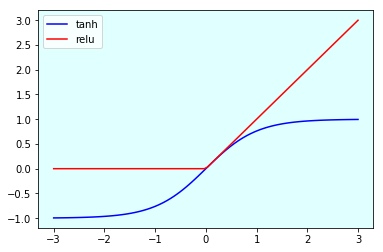
     Как мы видим, relu приравнивает отрицательные числа к 0, иначе не делает ничего.

Формула гиперболического тангенса до жути проста:

sinh(x) / cosh(x)

Гиперболический синус имеет следующий вид:

( (e ** x) - (e ** (-x)) ) / 2, где ** - оператор возведения в степень

Гиперболический косинус также очень схож:

( (e ** x) + (e ** (-x)) ) / 2, где ** - оператор возведения в степень

Делим первое на второе и получаем:

( e ** x - e ** (-x) ) / ( e ** x + e ** (-x) )

Если вынести в числителе и знаменателе e ** (-x) и сократить его, получаем рабочую формулу:

(e ** 2x - 1) / (e ** 2x + 1)

     Когда недавно впервые столкнулся с такими понятиями, задавал себе вопрос: что общего эти функции имеют с тригонометрией? Многие наверняка знают, так что пишу для "зеленых" : функции преобразования у гиперболических функций такие же, как и у тригонометрических.

Основные понятия

     Немного о базовых понятиях:

• Итерация - счетчик, который увеличивается каждый раз, когда нейросеть проходит один тренировочный сет.
• Эпоха - задаваемое программистом значение, которое при инициализации выставляется нулём, и увеличивается, когда "нейронка" проходит все тренировочные сеты.

Процесс инкремента эпохи и итерации:

• сначала n раз увеличивается итерация, затем эпоха. Результат подобен вложенному циклу:

• Ошибка - величина, которая является разницей между полученными и тестовыми результатами. Она устанавливается при каждом инкременте эпохи и каждый раз должна обучаться для хорошего обучения. Существуют три основных способа вычисления ошибки: средняя квадратичная ошибка(MSE), корневая средняя квадратичная ошибка и арктангенс.
• MSE(Mean Squared Error). Способ вычисления ошибки, который мы уже встречали при линейныхмоделях(коэффициенты вычисляются дабы уменьшить MSE). Формула(o - предсказанный результат, i - ожидаемый результат):

( (I1 - O1) ** 2 + (I2 - O2) ** 2 ... + (In - On) ** 2 ) / n

• Root Mean Squared Error. Та же самая MSE, только под корнем:

sqrt(( (I1 - O1) ** 2 + (I2 - O2) ** 2 + ... + (In - On) ** 2 ) / n)

• Arctan. Вычисление квадратичного тангенса и деление на кол-во сетов:

(arctan**2(I1 - O1) + arctan**2(I2 - O2) + ... + arctan**2(In - On) / n)

• Процесс обучения происходит за счет подбора весов для уменьшения ошибки. Есть один важный момент: первый раз веса задаются случайным образом, потому обучив две одинаковые модели на одном и том же наборе данных, вы можете получить разную обобщающую способность.

     Заключение. Нейронные сети - сверхважный алгоритм, потому надо в точности знать все тонкости его работы. Нейросети имеют очень тонкую настройку параметров(alpha для регуляризации, кол-во скрытых узлов и т.д.), потому стоит хорошо подумать, дабы отлично настроить свою модель. В следующей статье разберём практическое применение нейросети, реализованной в sklearn.

Источник: m.vk.com